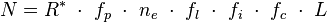lunes, 13 de enero de 2014
Esperemos que ninguno de nosotros tengamos que recurrir a la probabilidad esta tarde...
Un alumno del Master de Educación tiene que realizar un examen tipo test de 30 preguntas. Cada pregunta tiene 4 posibles respuestas. Supongamos que no ha estudiado nada y responde a las preguntas al azar. ¿Cuál es la probabilidad de que responda bien a más del 75% de las preguntas? ¿Y de que responga bien a todas? ¿Y de que responda mal a todas?
jueves, 9 de enero de 2014
¿Os suena el Gato de Schrödinger?
Erwin Schrödinger plantea un sistema que se encuentra formado por una
caja cerrada y opaca que contiene un gato en su interior, una botella
de gas venenoso y un dispositivo, el cual contiene una partícula
radiactiva con una probabilidad del 50% de desintegrarse en un tiempo
dado, de manera que si la partícula se desintegra, el veneno se libera y
el gato muere.
Al terminar el tiempo establecido, hay una probabilidad del 50% de que el dispositivo se haya activado y el gato esté muerto, y la misma probabilidad de que el dispositivo no se haya activado y el gato esté vivo. Según los principios de la mecánica cuántica, la descripción correcta del sistema en ese momento (su función de onda) será el resultado de la superposición de los estados «vivo» y «muerto» (a su vez descritos por su función de onda). Sin embargo, una vez que se abra la caja para comprobar el estado del gato, éste estará vivo o muerto.
Ahí radica la paradoja. Mientras que en la descripción clásica del sistema el gato estará vivo o muerto antes de que abramos la caja y comprobemos su estado, en la mecánica cuántica el sistema se encuentra en una superposición de los estados posibles hasta que interviene el observador. El paso de una superposición de estados a un estado definido se produce como consecuencia del proceso de medida, y no puede predecirse el estado final del sistema: solo la probabilidad de obtener cada resultado. La naturaleza del proceso sigue siendo una incógnita, que ha dado lugar a distintas interpretaciones de carácter especulativo.
Si bien esta paradoja resulta difícil de comprender para muchos y su interpretación es variada e inconstante, podemos ver algunas referencias al mismo en varias series, cómics y videojuegos actuales. Por otra parte, la popularidad de los gatos en las redes sociales ha generado una gran cantidad de chistes y bromas que refieren al experimento.
Al terminar el tiempo establecido, hay una probabilidad del 50% de que el dispositivo se haya activado y el gato esté muerto, y la misma probabilidad de que el dispositivo no se haya activado y el gato esté vivo. Según los principios de la mecánica cuántica, la descripción correcta del sistema en ese momento (su función de onda) será el resultado de la superposición de los estados «vivo» y «muerto» (a su vez descritos por su función de onda). Sin embargo, una vez que se abra la caja para comprobar el estado del gato, éste estará vivo o muerto.
Ahí radica la paradoja. Mientras que en la descripción clásica del sistema el gato estará vivo o muerto antes de que abramos la caja y comprobemos su estado, en la mecánica cuántica el sistema se encuentra en una superposición de los estados posibles hasta que interviene el observador. El paso de una superposición de estados a un estado definido se produce como consecuencia del proceso de medida, y no puede predecirse el estado final del sistema: solo la probabilidad de obtener cada resultado. La naturaleza del proceso sigue siendo una incógnita, que ha dado lugar a distintas interpretaciones de carácter especulativo.
Si bien esta paradoja resulta difícil de comprender para muchos y su interpretación es variada e inconstante, podemos ver algunas referencias al mismo en varias series, cómics y videojuegos actuales. Por otra parte, la popularidad de los gatos en las redes sociales ha generado una gran cantidad de chistes y bromas que refieren al experimento.
- En el episodio 171 de la sexta temporada de la serie animada Futurama una corta escena hace referencia a este experimento, cuando al abrir una caja Fry es atacado por un gato que estaba dentro y luego un robot que revisa la caja confirma que se trata de la caja de Schrödinger.
- Al final de la primera temporada de la popular serie The Big Bang Theory, Sheldon Cooper explica el experimento del gato de Schrödinger para compararlo con la situación sentimental de Penny y Leonard.
- Existe un manga japonés titulado Hellsing, de Kōta Hirano, donde se hace referencia al experimento con un personaje, precisamente llamado Schrödinger que posee rasgos felinos (incluso orejas) y que tiene la capacidad de trasladarse por diferentes universos o distorsiones de tiempo espacio, pudiendo estar en todos lados y al mismo tiempo en ningún lugar siendo así un personaje inmortal, siempre y cuando sea consciente de su propia existencia. Esto último refiere puntualmente a la interpretación de muchos mundos de Hugh Everett.
- En la serie de novelas liegras To Aru Majutsu no Index, de Kazuma Kamachi uno de los personajes hace referencia a este experimento para explicar como funcionan los poderes ESPER.
- En el manga Umineko no Naku Koro Ni el argumento se muestra como una paradoja haciendo referencia al gato de Schrödinger, ya que los personajes se encuentran en una isla en donde la historia se repite una y otra vez habiendo en cada una diferentes factores que hacen que haya infinita combinaciones de mundos.
- En el videojuego Bioshock Infinite aparece reflejada la esencia de este experimento durante varias secuencias del juego. Así lo deja entrever Ken Levine en respuesta a una consulta de un aficionado por Twitter.
- En el videojuego Virtue's Last Reward, se menciona en varias ocasiones la teoría de Schrödinger, constituyendo a uno de los argumentos principales de la trama.
- En la novela de título Sábado, de Ian Mc Ewan, se hace referencia cuando alude a las posibilidades de que existan supervivientes tras un accidente aéreo.
¿CUÁL ES LA PROBABILIDAD DE MORIR DE...?
Esta es una lista de posibles causas de muerte, y las diferentes probabilidades de cada una.
Contacto con serpientes venenosas — 1 entre 1.874.034
Contacto con arañas venenosas — 1 entre 468.508
Accidente con fuegos artificiales — 1 entre 340.733
Mordido o picado por insectos no venenosos — 1 entre 312.339
Accidente de tren — 1 entre 156.169
Inundación — 1 entre 144.156
Terremoto — 1 entre 117.127
Mordido o herido por un perro — 1 entre 117.127
Accidente de bus — 1 entre 104.113
Un rayo — 1 entre 79.746
Picadura de avispas — 1 entre 56.789
Exposición a excesivo calor natural — 1 entre 13.729
Ahogamiento accidental en la bañera — 1 entre 11.289
Intoxicación por Alcohol — 1 entre 10.048
Electrocutado accidentalmente — 1 entre 9.968
Asfixia u ahogamiento accidental en la cama — 1 entre 7.541
Ahogamiento accidental en una piscina — 1 entre 7.278
Exposición a excesivo frío natural — 1 entre 6.045
Disparo accidental por arma de fuego — 1 entre 5.134
Accidente aéreo o espacial — 1 entre 5.051
Accidente en bicicleta — 1 entre 4.919
Por caer de una cama, silla u otro mobiliario — 1 entre 4.473
Obstrucción del tracto respiratorio al ingerir comida — 1 entre 4.284
Al caer de unas escaleras — 1 entre 2.360
En un incendio incontrolado en un edificio — 1 entre 1.358
Complicaciones medicas tras una operación — 1 entre 1.313
Fuego o humo — 1 entre 1.113
Accidente de moto — 1 entre 1.020
Ahogado — 1 entre 1.008
Accidente peatonal — 1 entre 626
Estupefacientes y alucinógenos — 1 entre 406
Asalto con arma de fuego — 1 entre 314
Accidente de coche — 1 entre 237
Caída — 1 entre 218
Suicidio — 1 entre 119
Accidente con cualquier tipo de vehículo a motor — 1 entre 84
Embolia — 1 entre 24
Cáncer — 1 entre 7
Ataque al corazón — 1 entre 5
Por cualquier causa — 1 entre 1
Contacto con serpientes venenosas — 1 entre 1.874.034
Contacto con arañas venenosas — 1 entre 468.508
Accidente con fuegos artificiales — 1 entre 340.733
Mordido o picado por insectos no venenosos — 1 entre 312.339
Accidente de tren — 1 entre 156.169
Inundación — 1 entre 144.156
Terremoto — 1 entre 117.127
Mordido o herido por un perro — 1 entre 117.127
Accidente de bus — 1 entre 104.113
Un rayo — 1 entre 79.746
Picadura de avispas — 1 entre 56.789
Exposición a excesivo calor natural — 1 entre 13.729
Ahogamiento accidental en la bañera — 1 entre 11.289
Intoxicación por Alcohol — 1 entre 10.048
Electrocutado accidentalmente — 1 entre 9.968
Asfixia u ahogamiento accidental en la cama — 1 entre 7.541
Ahogamiento accidental en una piscina — 1 entre 7.278
Exposición a excesivo frío natural — 1 entre 6.045
Disparo accidental por arma de fuego — 1 entre 5.134
Accidente aéreo o espacial — 1 entre 5.051
Accidente en bicicleta — 1 entre 4.919
Por caer de una cama, silla u otro mobiliario — 1 entre 4.473
Obstrucción del tracto respiratorio al ingerir comida — 1 entre 4.284
Al caer de unas escaleras — 1 entre 2.360
En un incendio incontrolado en un edificio — 1 entre 1.358
Complicaciones medicas tras una operación — 1 entre 1.313
Fuego o humo — 1 entre 1.113
Accidente de moto — 1 entre 1.020
Ahogado — 1 entre 1.008
Accidente peatonal — 1 entre 626
Estupefacientes y alucinógenos — 1 entre 406
Asalto con arma de fuego — 1 entre 314
Accidente de coche — 1 entre 237
Caída — 1 entre 218
Suicidio — 1 entre 119
Accidente con cualquier tipo de vehículo a motor — 1 entre 84
Embolia — 1 entre 24
Cáncer — 1 entre 7
Ataque al corazón — 1 entre 5
Por cualquier causa — 1 entre 1
Paradoja de Fermi
La paradoja de Fermi es la contradicción entre las
estimaciones que afirman que hay una alta probabilidad de existencia de
civilizaciones inteligentes en el universo, y la ausencia de evidencia
de dichas civilizaciones. Surgió en 1950 en medio de una conversación
informal del físico Enrico Fermi
con otros físicos del laboratorio pero ha tenido importantes
implicaciones en los proyectos de búsquedas de señales de civilizaciones
extraterrestres (SETI).
Trata de responder a la pregunta: «¿Somos los seres humanos la única civilización avanzada en el Universo?» La ecuación de Drake para estimar el número de civilizaciones extraterrestres con las que finalmente podríamos ponernos en contacto parece implicar que tal tipo de contacto no es extremadamente raro. La respuesta de Fermi a esta conclusión es que si hubiera numerosas civilizaciones avanzadas en nuestra galaxia entonces «¿Dónde están? ¿Por qué no hemos encontrado trazas de vida extraterrestre inteligente, por ejemplo, sondas, naves espaciales o transmisiones?» Aquéllos que se adhieren a las conclusiones de Fermi suelen referirse a esta premisa como el Principio de Fermi.
La paradoja puede resumirse de la manera siguiente: La creencia común de que el Universo posee numerosas civilizaciones avanzadas tecnológicamente, combinada con nuestras observaciones que sugieren todo lo contrario es paradójica sugiriendo que nuestro conocimiento o nuestras observaciones son defectuosas o incompletas.
La formulación de la paradoja surgió en una época en la que Fermi estaba trabajando en el Proyecto Manhattan cuyo fin era el desarrollo de la bomba atómica estadounidense. La respuesta de Fermi a su paradoja es que toda civilización avanzada desarrollada en la galaxia, desarrolla con su tecnología el potencial de exterminarse tal y como percibía que estaba ocurriendo en su época. El hecho de no encontrar otras civilizaciones extraterrestres implicaba para él un trágico final para la humanidad.
Trata de responder a la pregunta: «¿Somos los seres humanos la única civilización avanzada en el Universo?» La ecuación de Drake para estimar el número de civilizaciones extraterrestres con las que finalmente podríamos ponernos en contacto parece implicar que tal tipo de contacto no es extremadamente raro. La respuesta de Fermi a esta conclusión es que si hubiera numerosas civilizaciones avanzadas en nuestra galaxia entonces «¿Dónde están? ¿Por qué no hemos encontrado trazas de vida extraterrestre inteligente, por ejemplo, sondas, naves espaciales o transmisiones?» Aquéllos que se adhieren a las conclusiones de Fermi suelen referirse a esta premisa como el Principio de Fermi.
La paradoja puede resumirse de la manera siguiente: La creencia común de que el Universo posee numerosas civilizaciones avanzadas tecnológicamente, combinada con nuestras observaciones que sugieren todo lo contrario es paradójica sugiriendo que nuestro conocimiento o nuestras observaciones son defectuosas o incompletas.
La formulación de la paradoja surgió en una época en la que Fermi estaba trabajando en el Proyecto Manhattan cuyo fin era el desarrollo de la bomba atómica estadounidense. La respuesta de Fermi a su paradoja es que toda civilización avanzada desarrollada en la galaxia, desarrolla con su tecnología el potencial de exterminarse tal y como percibía que estaba ocurriendo en su época. El hecho de no encontrar otras civilizaciones extraterrestres implicaba para él un trágico final para la humanidad.
ECUACIÓN DE DRAKE...¿CUÁL ES LA PROBABILIDAD DE QUE EXISTA VIDA EXTRATERRESTRE?
La ecuación de Drake o fórmula de Drake fue concebida por el radioastrónomo y presidente del Instituto SETI Frank Drake, con el propósito de estimar la cantidad de civilizaciones en nuestra galaxia, la Vía Láctea, susceptibles de poseer emisiones de radio detectables.
La ecuación fue concebida en 1961 por Drake mientras trabajaba en el Observatorio de Radioastronomía Nacional en Green Bank, Virginia Occidental (EE. UU.). La ecuación de Drake identifica los factores específicos que, se cree, tienen un papel importante en el desarrollo de las civilizaciones. Aunque en la actualidad no hay datos suficientes para resolver la ecuación, la comunidad científica ha aceptado su relevancia como primera aproximación teórica al problema, y varios científicos la han utilizado como herramienta para plantear distintas hipótesis.
Nuestro sol es sólo una estrella solitaria en la abundancia de 7×1022 estrellas en el universo observable.1 La Vía Láctea es tan sólo una de entre las 500.000.000.000 galaxias del Universo. Parece que debería haber un montón de vida ahí fuera.
El primero en hacer una estimación inicial fue el astrónomo Frank Drake. Éste concibió una ecuación, ahora conocida como Ecuación de Drake, basada en varios parámetros:
La ecuación fue concebida en 1961 por Drake mientras trabajaba en el Observatorio de Radioastronomía Nacional en Green Bank, Virginia Occidental (EE. UU.). La ecuación de Drake identifica los factores específicos que, se cree, tienen un papel importante en el desarrollo de las civilizaciones. Aunque en la actualidad no hay datos suficientes para resolver la ecuación, la comunidad científica ha aceptado su relevancia como primera aproximación teórica al problema, y varios científicos la han utilizado como herramienta para plantear distintas hipótesis.
Nuestro sol es sólo una estrella solitaria en la abundancia de 7×1022 estrellas en el universo observable.1 La Vía Láctea es tan sólo una de entre las 500.000.000.000 galaxias del Universo. Parece que debería haber un montón de vida ahí fuera.
El primero en hacer una estimación inicial fue el astrónomo Frank Drake. Éste concibió una ecuación, ahora conocida como Ecuación de Drake, basada en varios parámetros:
 es el ritmo anual de formación de estrellas "adecuadas" en la galaxia.
es el ritmo anual de formación de estrellas "adecuadas" en la galaxia. es la fracción de estrellas que tienen planetas en su órbita.
es la fracción de estrellas que tienen planetas en su órbita.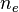 es el número de esos planetas orbitando dentro de la ecosfera
de la estrella (las órbitas cuya distancia a la estrella no sea tan
próxima como para ser demasiado calientes, ni tan lejana como para ser
demasiado frías para poder albergar vida).
es el número de esos planetas orbitando dentro de la ecosfera
de la estrella (las órbitas cuya distancia a la estrella no sea tan
próxima como para ser demasiado calientes, ni tan lejana como para ser
demasiado frías para poder albergar vida).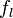 es la fracción de esos planetas dentro de la ecosfera en los que la vida se ha desarrollado.
es la fracción de esos planetas dentro de la ecosfera en los que la vida se ha desarrollado.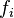 es la fracción de esos planetas en los que la vida inteligente se ha desarrollado.
es la fracción de esos planetas en los que la vida inteligente se ha desarrollado.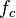 es la fracción de esos planetas donde la vida inteligente ha desarrollado una tecnología e intenta comunicarse.
es la fracción de esos planetas donde la vida inteligente ha desarrollado una tecnología e intenta comunicarse. es el lapso, medido en años, durante el que una civilización inteligente y comunicativa puede existir.
es el lapso, medido en años, durante el que una civilización inteligente y comunicativa puede existir.
- R* = 10/año (10 estrellas se forman cada año)
- fp = 0.5 (La mitad de esas estrellas cuentan con planetas)
- ne = 2 (Cada una de esas estrellas contiene 2 planetas)
- fl = 1 (El 100% de esos planetas podría desarrollar vida)
- fi = 0.01 (Solo el 1% albergaría vida inteligente)
- fc = 0.01 (Solo el 1% de tal vida inteligente se puede comunicar)
- L = 10.000 años (Cada civilización duraría 10.000 años trasmitiendo señales)
- N = 10 × 0.5 × 2 × 1 × 0.01 × 0.01 × 10,000
- N = 10 posibles civilizaciones detectables.
miércoles, 8 de enero de 2014
LOTERÍA Y PROBABILIDAD...TE PUEDE TOCAR A TÍ ;)
En 3º de ESO muchos serán los alumnos que afirmen que la Probabilidad, al igual que todo lo que tiene que ver con las Matemáticas y los estudios en general, es algo inutil. Quizás si les enseñaís esto les demostreis que son más útiles de lo que ellos creen.
LOTERIAS DE ESPAÑA
Pocas personas podrán decir que se han resistido
a la tentación de probar suerte con algún juego de azar, como
lo atestigua todos los años el balance económico de Loterías
y Apuestas del Estado. En 2005 los españoles se gastaron más
de 28 mil millones de euros en juegos de azar, que una vez
descontados los premios, daría lugar a un gasto efectivo de
nueve mil millones de euros. Esto supone un consumo
per cápita de 642 euros y las ventas en el 2006 aumentaron
un 5,54 %.
Un 60% de esta cantidad corresponde a los juegos privados (tragaperras, casinos y bingos), otro 33% a loterías públicas y un 7% a los juegos de la ONCE .
Los españoles podrían programar sus apuestas en función de las probabilidades pero, para esto, tendrían que analizar los índices de cada uno de los sorteos existentes. De mayor a menor, las probabilidades de tener más suerte y ganar son las siguientes:
- La Lotería Nacional, en el sorteo de los jueves, la probabilidad es de 1 entre 600.000, y en el sorteo de navidad , la probabilidad es de 1 entre 85.000.
- Seguida a mayor distancia de la Quiniela, que para llevarse el pleno, la probabilidad es de uno entre casi cinco millones.
- La suerte de ganar el premio mayor con la Lotería Primitiva es de uno entre 14 millones. Le sigue El Cuponazo, con una probabilidad de uno entre 15 millones.
- Luego se sitúa El Gordo de la Primitiva con una probabilidad de llevarse el primer premio de 1 entre unos 31 millones y por último El Euromillón, con una probabilidad de uno entre 76 millones.
En cuanto a los juegos que más pasiones levantan destaca sin duda la Lotería Nacional, con una participación del 57%; seguida por la Primitiva, con el 25%; la Bono Loto, con el 7%; la Quiniela con el 6% y, por último, El Gordo de la Primitiva, con el 4%.
Vamos a hacer un estudio detallado de cada una de las probabilidaddes de las distintas loterias nacionales:
-
 La Primitiva y la Bono
Loto » 1 entre 13.983.816
La Primitiva y la Bono
Loto » 1 entre 13.983.816
-
 El
Gordo de la Primitiva »1 entre 31.625.100
El
Gordo de la Primitiva »1 entre 31.625.100
-
 Euromillones
» 1 entre 76.275.360
Euromillones
» 1 entre 76.275.360
-
 Lotería
Nacional » 1 entre 600.000(Jueves)1
entre 85.000(Navidad)
Lotería
Nacional » 1 entre 600.000(Jueves)1
entre 85.000(Navidad)
-

 La Quiniela y el Quinigol » 1 entre 4.782.969
La Quiniela y el Quinigol » 1 entre 4.782.969
-

 Hípica nacional »
1 entre 8.835.372 (Lototurf)
Hípica nacional »
1 entre 8.835.372 (Lototurf)
1 entre 60.080.000 (Quíntuple Plus) -
 Cupón
Once » 1 entre 15 millones
Cupón
Once » 1 entre 15 millones -
 El Combo
de la Once »1 entre 15 millones
El Combo
de la Once »1 entre 15 millones
CLAVES PRÁCTICAS PARA ESTUDIAR ESTADISTICA!!!!
Muchos estudiantes tienen dificultad para aprender Probabilidad, aquí tienen algunas claves para triunfar a la hora de estudiar probabilidad.
- LEA CUIDADOSAMENTE Y DELIBERADAMENTE. La forma en que usted debe leer en las estadísticas es muy diferente de la manera que usted puede leer un libro de historia, un periódico o una novela. En las estadísticas, debe leer lentamente, absorbiendo cada palabra. A veces es necesario para leer un libro de texto o discusión de un problema muchas veces antes de que comience a "dar sentido" a usted. En algunos tipos de lectura, como una novela, es conveniente leerlo y leer rápidamente, porque por lo general hay un par de pensamientos "salpicados" entre muchas palabras. Sin embargo, en las estadísticas de lectura de cada palabra o símbolo es importante porque hay muchos pensamientos condensados en algunas declaraciones. Tenga en cuenta que las pequeñas palabras significan mucho en las estadísticas.
- PENSAR CON EL LÁPIZ Y PAPEL . Tenga siempre un lápiz en la mano y papel borrador listo y utilizarlos cuando lees y estudias las estadísticas. Pruebe las ideas en papel que los autores están discutiendo. Cuando se proponen una pregunta, tratar de responder antes de pasar. A pesar de que un ejemplo puede ser resuelto por completo en el texto, el trabajo por ti mismo en el papel de cero. Esto ayudará a afianzar las ideas y los procedimientos en su mente antes de comenzar los ejercicios. Después de haber leído y releído un problema con cuidado, si tu todavía no ven qué hacer, no sólo sentarse y mirar. Obtenga su lápiz pasando de cero papel y tratar de "sacarlo. Si, en el intento de resolver un problema, vou tiene nada escrito en papel. Entonces por lo general usted todavía no ha ejercido suficiente esfuerzo para justificar la búsqueda de ayuda.
- SER INDEPENDIENTE. Trata de completar cada lección sin ayuda. Si vou buscar ayuda sin necesidad, ya sea de su profesor, un compañero de clase, el manual de soluciones, o el laboratorio de matemáticas, usted no va a ganar el máximo beneficio de su trabajo. Se necesita hacer ejercicio, ya sabes, para ser fuerte. No se puede aprender las estadísticas a través del ejercicio de otro. Sin embargo, debe hacer preguntas cuando sea necesario. A veces las pequeñas cosas hacen una gran confusión. No tenga miedo de que tu pregunta puede sonar "tonto". La única acción "tonto" es dejar de preguntar acerca de un tema que vou realmente han tratado de captar y todavía no entiendo. Algunas personas buscan ayuda demasiado pronto y algunos esperan demasiado tiempo. Usted tendrá que utilizar el sentido común en este asunto.
- ESCUCHAR EN CLASE. Muchos de los puntos más finos. principios y modos de pensamiento fundamentales serán desarrolladas en clase. Debe prestar especial atención a estas actividades con el fin de entender realmente lo que está pasando.
- PERSEVERAR. No se frustre si un tema o problema que pueden desconcertar por completo al principio. Palo con ella! Una característica muy interesante de las estadísticas sobre aprendizaje es que en un momento el alumno puede sentirse totalmente a pérdida, y de repente tener una ráfaga de intuición que le permite comprender perfectamente la situación. El aprendizaje no es un proceso de "todo" o "nada"! Si usted no parece estar haciendo ningún progreso después de trabajar en un problema desde hace algún tiempo, ponerlo a un lado y atacar de nuevo más tarde. Muchas veces usted verá inmediatamente la solución de inmediato a pesar de que usted no ha sido conscientemente pensando en el problema en el ínterin. Hay un gran sentido de satisfacción por haber sido lo suficientemente persistente y suficiente para resolver independientemente un problema que había dado una gran cantidad de problemas creativa.
- REFLEXIONAR. Para conocer las estadísticas, así que usted debe tomar tiempo para hacer un poco de pensamiento reflexivo sobre el material cubierto en los últimos días o semanas. Se necesita tiempo para obtener algunas ideas en las estadísticas de "remojo" in "Puede que tenga que vivir con ellos un tiempo y hacer el pensamiento reflexivo sobre ellos antes de que se conviertan en una parte de ti.
- CONCENTRARSE. No trate de aprender estadísticas memorizando ejemplos ilustrativos. Usted pronto se sienten abrumados por este enfoque, y cuanto más se vaya, menos éxito tendrá. El campo de la estadística se basa en un número sorprendentemente pequeño de principios y definiciones fundamentales. La mayoría de éstos debe ser memorizada. Pero si usted se concentra en estos fundamentos y tratar de ver cómo cada nuevo tema es sólo una solicitud y / o la extensión de ellos, será necesario muy poca memorización adicional.
- SER ORDENADO. Estos son hábitos que le ahorrará muchos dolores de cabeza "" En cualquier campo de actividad. La mayoría de las personas deben practicar deliberadamente pulcritud y precisión antes de que se conviertan en un hábito. Mantenga su trabajo organizado. Tienen una sección especial en su cuaderno para las estadísticas. Mantenga cada tarea (junto con las pruebas de edad, notas, etc) en un lugar céntrico para que pueda referirse a ellos cuando sea necesario.
- TOMARSE SU TIEMPO. Usted debe hacer sus tareas con regularidad y recuperar el trabajo perdido en su ausencia. No espere hasta el último minuto para hacer su trabajo y luego correr a través de él. Si usted pasa tiempo suficiente en su lección para obtener las "respuestas" y no se toman el tiempo para realmente entender los principios subyacentes, que pronto se confunden. Las estadísticas pueden ser agradables, siempre y cuando usted está "en la parte superior de la misma" y que entiende lo que está pasando, de lo contrario, es muy frustrante.
La Aguja de Buffon
Una manera que conocemos para calcular el valor de  es trazando un círculo y dividiendo lo
que mide su circunferencia entre lo que mide su diámetro.
Sin embargo, desde hace cientos de años, los matemáticos han
desarrollado otras maneras para llegar al número
es trazando un círculo y dividiendo lo
que mide su circunferencia entre lo que mide su diámetro.
Sin embargo, desde hace cientos de años, los matemáticos han
desarrollado otras maneras para llegar al número  .
.
 Marca muy bien el
doblez y corta la hoja. Es importante que lo hagas con cuidado
para que los dobleces que haremos luego no queden chuecos.
Marca muy bien el
doblez y corta la hoja. Es importante que lo hagas con cuidado
para que los dobleces que haremos luego no queden chuecos.
Ahora sí, toma tu mitad de hoja y… a doblar. Vamos a marcar siete dobleces en la hoja. Empieza por doblar por la mitad. Recuerda que lo puedes hacer procurando que la orilla l1 coincida con la l2 . Este doblez nos genera una nueva línea a la que llamaremos l3 .


 Ahora, desdobla
y vuelve a doblar de manera que las orillas l1
y l2 queden sobre la l3.
Ahora, desdobla
y vuelve a doblar de manera que las orillas l1
y l2 queden sobre la l3.

 Deja la hoja doblada
y, otra vez, haz que ambas orillas coincidan con la línea
de en medio. Recuerda marcar con cuidado los dobleces. Si
desdoblas la hoja verás que ya habrás trazado los siete dobleces.
Deja la hoja doblada
y, otra vez, haz que ambas orillas coincidan con la línea
de en medio. Recuerda marcar con cuidado los dobleces. Si
desdoblas la hoja verás que ya habrás trazado los siete dobleces.

 Lo que hicimos con
todo este doblar fue trazar en la hoja líneas paralelas entre
sí. Para que las puedas ver mejor, puedes remarcar las líneas
con una regla y un lápiz . Ya que sacaste la regla, fíjate
que la distancia entre las líneas siempre es la misma.
Lo que hicimos con
todo este doblar fue trazar en la hoja líneas paralelas entre
sí. Para que las puedas ver mejor, puedes remarcar las líneas
con una regla y un lápiz . Ya que sacaste la regla, fíjate
que la distancia entre las líneas siempre es la misma.
Corta el palillo de manera que su longitud sea exactamente igual a la distancia entre las líneas. Es importante que lo cortes de este tamaño, de lo contrario no te va a salir el experimento. Listo, ya podemos empezar…
La siguiente parte de la actividad simplemente consiste en dejar caer el palillo sobre la hoja muchas veces. Cada vez que lanzamos el palillo puede ocurrir una de dos cosas: que cruce alguna de las líneas o que no cruce ninguna de las líneas. ¿Podrías decir por qué el palillo no podría cruzar dos líneas al mismo tiempo?
Cada vez que lances
el palillo anota una rayita en la casilla marcada como Número
de lanzamientos ( N ) y cada vez que el
palillo cruce una de las líneas, anota una rayita en la casilla
Número de cruces ( N' ) . Por ejemplo,
cuando lances el palillo y éste cruza una línea anota una
rayita en la casilla N y otra rayita en la casilla
N'. Si, en cambio, arrojas el palillo y no cruza
ninguna línea, anota una rayita en la N y no anotes
nada en la N'.
Comienza a lanzar el palillo sobre la hoja. Procura hacerlo el mayor número de veces posible. Si puedes hacerlo cien veces o más, qué mejor.
Ahora vamos a hacer un pequeño cálculo. Toma la cantidad de veces que arrojaste el palillo (el número de rayitas que hay en la casilla L) y multiplícala por dos. A lo que te quedó, divídelo entre el número de cruces (el número de rayitas que hay en la casilla C). ¿Tu resultado se parece a 3.141592…?
Si no se parece, seguro que no lanzaste el palillo el número suficiente de veces. Sigue lanzando y verás que en algún momento el resultado que obtengas sí se parecerá mucho al valor de .
.
Igual de sorprendido quedó el Conde de Buffon hace más de doscientos años cuando descubrió que se puede obtener una muy buena aproximación de lanzando palillos
sobre una hoja llena de rayas.
lanzando palillos
sobre una hoja llena de rayas.
La fórmula para obtener una aproximación de queda entonces
así:
queda entonces
así:
 = 2N/N'
Recuerda que:
= 2N/N'
Recuerda que:
Si se tira la aguja sobre la superficie puede que esta corte o no a alguna de las líneas. Consideramos como favorable aquel lanzamiento en el que la aguja efectivamente cae sobre alguna de ellas.
Pues bien: lo que demostró matemáticamente Buffon es que la probabilidad de que un lanzamiento sea favorable en este sentido es igual a 2l/dπ . Es evidente entonces que si hacemos l y d iguales la probabilidad será 2/π.
Por otra parte, si llamamos N al número de lanzamientos y N' al número de casos favorables, el cociente N'/N se aproximará a dicha probabilidad a medida que N aumente. Por lo tanto, si tiramos la aguja un número grande de veces podremos escribir:

"La Aguja de Buffon"
Este experimento propuesto por el Conde de Buffon en 1777 consiste en dejar caer una aguja sobre una hoja rayada y anotar las veces que la aguja cruza alguna de las rayas. Después de lanzar la aguja muchísimas veces comprobó que su experimento estaba íntimamente relacionado con el número . Para obtener un número muy parecido
a
. Para obtener un número muy parecido
a  , hay que dejar caer la aguja muchísimas
veces sobre la hoja, multiplicar esta cantidad por dos y dividir
el resultado entre el número de veces que la aguja cruzó alguna
de las rayas.
, hay que dejar caer la aguja muchísimas
veces sobre la hoja, multiplicar esta cantidad por dos y dividir
el resultado entre el número de veces que la aguja cruzó alguna
de las rayas.
Con el llamado "problema de la aguja de Buffon", (siglo
XVIII ), nace la teoría de las probabilidades geométricas
desarrollada poco después por
Laplace » en su gran tratado "Teoría analítica de las
probabilidades" (1812).Este experimento propuesto por el Conde de Buffon en 1777 consiste en dejar caer una aguja sobre una hoja rayada y anotar las veces que la aguja cruza alguna de las rayas. Después de lanzar la aguja muchísimas veces comprobó que su experimento estaba íntimamente relacionado con el número
 . Para obtener un número muy parecido
a
. Para obtener un número muy parecido
a  , hay que dejar caer la aguja muchísimas
veces sobre la hoja, multiplicar esta cantidad por dos y dividir
el resultado entre el número de veces que la aguja cruzó alguna
de las rayas.
, hay que dejar caer la aguja muchísimas
veces sobre la hoja, multiplicar esta cantidad por dos y dividir
el resultado entre el número de veces que la aguja cruzó alguna
de las rayas. Realizamos el experimento
Te invitamos a repetir el experimento. Necesitamos un palillo y una hoja blanca. En realidad no necesitamos la hoja entera, sólo la mitad. Para poder cortar la hoja por la mitad hay que doblarla de manera que la orilla AB quede exactamente sobre la orilla CD, el punto A sobre el C y el punto B sobre el D; así:
Ahora sí, toma tu mitad de hoja y… a doblar. Vamos a marcar siete dobleces en la hoja. Empieza por doblar por la mitad. Recuerda que lo puedes hacer procurando que la orilla l1 coincida con la l2 . Este doblez nos genera una nueva línea a la que llamaremos l3 .







Corta el palillo de manera que su longitud sea exactamente igual a la distancia entre las líneas. Es importante que lo cortes de este tamaño, de lo contrario no te va a salir el experimento. Listo, ya podemos empezar…
La siguiente parte de la actividad simplemente consiste en dejar caer el palillo sobre la hoja muchas veces. Cada vez que lanzamos el palillo puede ocurrir una de dos cosas: que cruce alguna de las líneas o que no cruce ninguna de las líneas. ¿Podrías decir por qué el palillo no podría cruzar dos líneas al mismo tiempo?
| Número de lanzamientos N: |
| Número de cruces N': |
Comienza a lanzar el palillo sobre la hoja. Procura hacerlo el mayor número de veces posible. Si puedes hacerlo cien veces o más, qué mejor.
Ahora vamos a hacer un pequeño cálculo. Toma la cantidad de veces que arrojaste el palillo (el número de rayitas que hay en la casilla L) y multiplícala por dos. A lo que te quedó, divídelo entre el número de cruces (el número de rayitas que hay en la casilla C). ¿Tu resultado se parece a 3.141592…?
Si no se parece, seguro que no lanzaste el palillo el número suficiente de veces. Sigue lanzando y verás que en algún momento el resultado que obtengas sí se parecerá mucho al valor de
Igual de sorprendido quedó el Conde de Buffon hace más de doscientos años cuando descubrió que se puede obtener una muy buena aproximación de
La fórmula para obtener una aproximación de
- N es el número de veces que lanzas el palillo (lanzamientos),
- N' es el número de veces que el palillo cruza alguna de las líneas (cruces)
- Cuántas más veces dejes caer el palillo sobre la hoja,
más se parecerá tu resultado a
 .
. - Esto funciona siempre y cuando lancemos el palillo de modo realmente aleatorio. Podría sorprendernos la tendencia que tenemos a repetir, si nada nos lo impide, los mismos gestos.
Justificamos el resultado
Supongamos que disponemos de una superficie rayada con líneas paralelas y una aguja de tal modo que si la aguja tiene una longitud l, la distancia d que separa a todas las paralelas es mayor que l.Si se tira la aguja sobre la superficie puede que esta corte o no a alguna de las líneas. Consideramos como favorable aquel lanzamiento en el que la aguja efectivamente cae sobre alguna de ellas.
Pues bien: lo que demostró matemáticamente Buffon es que la probabilidad de que un lanzamiento sea favorable en este sentido es igual a 2l/dπ . Es evidente entonces que si hacemos l y d iguales la probabilidad será 2/π.
Por otra parte, si llamamos N al número de lanzamientos y N' al número de casos favorables, el cociente N'/N se aproximará a dicha probabilidad a medida que N aumente. Por lo tanto, si tiramos la aguja un número grande de veces podremos escribir:
De donde, despejando, se tiene:

HISTORIA DE LA PROBABILIDAD
En cuanto al concepto en sí, la probabilidad y el azar siempre
ha estado en la mente del ser humano. Por ejemplo:
Christian Huygens conoció la correspondencia entre Blaise Pascal y Pierre Fermat suscitada por el caballero De Méré, se planteó el debate de determinar la probabilidad de ganar una partida, y publicó (en 1657) el primer libro sobre probabilidad: De Ratiociniis in Ludo Aleae, (Calculating in Games of Chance), un tratado sobre juegos de azar.Se aceptaba como intuitivo el concepto de equiprobabilidad, se admitía que la probabilidad de conseguir un acontecimiento fuese igual al cociente entre
Durante el siglo XVIII, debido muy particularmente a la popularidad de los juegos de azar, el cálculo de probabilidades tuvo un notable desarrollo sobre la base de la anterior definición de probabilidad. Destacan en 1713 el teorema de Bernoulli y la distribución binomial, y en 1738 el primer caso particular estudiado por De Moivre » , del teorema central del límite. En 1809 Gauss » inició el estudio de la teoría de errores y en 1810 Laplace, que había considerado anteriormente el tema, completó el desarrollo de esta teoría. En 1812 Pierre Laplace » publicó Théorie analytique des probabilités en el que expone un análisis matemático sobre los juegos de azar.
A mediados del siglo XIX, un fraile agustino austríaco, Gregor Mendel, inició el estudio de la herencia, la genética, con sus interesantes experimentos sobre el cruce de plantas de diferentes características. Su obra, La matemática de la Herencia, fue una de las primeras aplicaciones importantes de la teoría de probabilidad a las ciencias naturales
Desde los orígenes la principal dificultad para poder considerar la probabilidad como una rama de la matemática fue la elaboración de una teoría suficientemente precisa como para que fuese aceptada como una forma de matemática. A principios del siglo XX el matemático ruso Andrei Kolmogorov » la definió de forma axiomática y estableció las bases para la moderna teoría de la probabilidad que en la actualidad es parte de una teoría más amplia como es la teoría de la medida.
- Sumerios y Asirios utilizaban un hueso extraído del talón de animales como ovejas, ciervos o caballos, denominado astrágalo o talus, que tallaban para que pudieran caer en cuatro posiciones distintas, por lo que son considerados como los precursores de los dados.
- En el caso de la civilización egipcia, algunas pinturas encontradas en las tumbas de los faraones muestran tanto astrágalos como tableros para el registro de los resultados.
- Por su parte, los juegos con dados se practicaron ininterrumpidamente desde los tiempos del Imperio Romano hasta el Renacimiento, aunque no se conoce apenas las reglas con las que jugaban. Uno de estos juegos, denominado "hazard", palabra que en inglés y francés significa riesgo o peligro, fue introducido en Europa con la Tercera Cruzada. Las raíces etimológicas del término provienen de la palabra árabe "al-azar", que significa "dado". Posteriormente, en el "Purgatorio" de Dante el término aparece ya como "azar".
- En la actualidad, ruletas, máquinas tragaperras, loterías, quinielas,..., nos indican que dicha fascinación del hombre por el juego, continúa.
Christian Huygens conoció la correspondencia entre Blaise Pascal y Pierre Fermat suscitada por el caballero De Méré, se planteó el debate de determinar la probabilidad de ganar una partida, y publicó (en 1657) el primer libro sobre probabilidad: De Ratiociniis in Ludo Aleae, (Calculating in Games of Chance), un tratado sobre juegos de azar.Se aceptaba como intuitivo el concepto de equiprobabilidad, se admitía que la probabilidad de conseguir un acontecimiento fuese igual al cociente entre
Durante el siglo XVIII, debido muy particularmente a la popularidad de los juegos de azar, el cálculo de probabilidades tuvo un notable desarrollo sobre la base de la anterior definición de probabilidad. Destacan en 1713 el teorema de Bernoulli y la distribución binomial, y en 1738 el primer caso particular estudiado por De Moivre » , del teorema central del límite. En 1809 Gauss » inició el estudio de la teoría de errores y en 1810 Laplace, que había considerado anteriormente el tema, completó el desarrollo de esta teoría. En 1812 Pierre Laplace » publicó Théorie analytique des probabilités en el que expone un análisis matemático sobre los juegos de azar.
A mediados del siglo XIX, un fraile agustino austríaco, Gregor Mendel, inició el estudio de la herencia, la genética, con sus interesantes experimentos sobre el cruce de plantas de diferentes características. Su obra, La matemática de la Herencia, fue una de las primeras aplicaciones importantes de la teoría de probabilidad a las ciencias naturales
Desde los orígenes la principal dificultad para poder considerar la probabilidad como una rama de la matemática fue la elaboración de una teoría suficientemente precisa como para que fuese aceptada como una forma de matemática. A principios del siglo XX el matemático ruso Andrei Kolmogorov » la definió de forma axiomática y estableció las bases para la moderna teoría de la probabilidad que en la actualidad es parte de una teoría más amplia como es la teoría de la medida.
Suscribirse a:
Entradas (Atom)